Public Key Cryptography: RSA

• Introduction
• Mathematical Background
• The Algorithm
  • Key Generation
  • Encryption
  • Decryption
• Implementation
  • Java (BigInteger)
    • Setup
    • Key Generation
    • Encryption and Decryption
  • Java with java-gmp
  • Python (gmpy2)
• The Mathy Bit
  • Group Theoretic Results
  • Correctness of RSA
  • Fermat’s Little Theorem
  • Euler’s Theorem
• Security of RSA

GitHub Project

Introduction

RSA is one of the first public-key cryptosystems, whose security relies on the conjectured intractability of the factoring problem. It was designed in 1977 by Ron Rivest, Adi Shamir, and Leonard Adleman (hence the name). You may read the original RSA paper here. While many people believe RSA to be the first public-key encryption, British mathematician Clifford Cocks invented an algorithm equivalent to RSA earlier in 1973, but this remained classified until 1997.

Asymmetric (public-key) cryptography relies heavily on number theoretic functions, and it is quite different from symmetric algorithms such as DES or AES. In a symmetric system, the same secret key is used for both encryption and decryption.

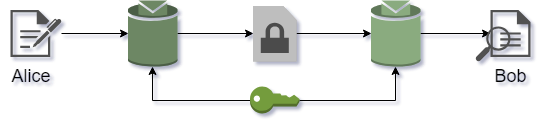Figure 1: Principle of symmetric-key encryption

This means that if Alice and Bob want to communicate using private-key encryption, they must find a way to establish the secret key over a secure channel first. This is known as the key distribution problem. Furthermore, the number of keys can become large fast: if we require each pair of users to have a separate pair of keys, a network with $n$ users would need a total of $$ \stc{n}{2} = \frac{n\cdot(n-1)}{2} $$ key pairs. For a corporation comprised of 1000 people, this amounts to about half a million keys that need to be generated and distributed securely to the individuals. Increase the number of users to 2000, and we’re looking at 2 million keys in total.

Asymmetric encryption overcomes these drawbacks (and a few others), as keys can be generated on the fly and the public key can be shared over insecure channels. In this article we will discuss the underlying mathematical theory, implement the unpadded RSA algorithm, and prove its correctness.

Mathematical Background

The mathematics behind RSA can be elegantly stated in the language of group theory. For simplicity, we introduce two classical theorems that are at the heart of the algorithm. The first one is due to Pierre de Fermat:

Theorem (Fermat’s Little Theorem, 1640) Suppose $p$ is prime and $a$ is any integer. Then $$ a^p \equiv a \md p. $$

This was first proved by Euler about a hundred years later, in 1736. Euler continued exploring the topic, and eventually provided the following generalization:

Theorem (Euler’s Theorem, 1763) Suppose $a$ and $n$ are coprime positive integers. Then $$ a^{\phi(n)} \equiv 1 \md n. $$

Here $\phi(n)$ is Euler’s totient function, which is defined as $$ \phi(n) = \text{# of positive integers less than $n$ that are relatively prime to $n$}. $$

We provide proofs for these theorems in the mathy bit section. For implementing RSA, we need to know the following properties of $\phi$:

• for any prime $p$, we have $\phi(p) = p-1$, and
• for distinct primes $p$ and $q$, $$ \phi(pq) = \phi(p) \phi(q) = (p-1)(q-1), $$

both of which can be easily derived using a counting argument.

The Algorithm

There are three main steps involved in RSA encryption:

• Public and secret key generation
• Encryption
• Decryption

Key Generation

Choose $p$ and $q$ to be two distinct (and large) primes, and compute $$ n = pq \quad \text{and} \quad \phi = \phi(n) = (p-1)(q-1). $$

To construct the public key, find any element $1 < e < \phi(n)$ that is coprime to $\phi$, so that $e$ is an element of the group $\zmods{\phi}$. The public key is the pair $(n, e)$.

To find the secret key, take the inverse of $e$ in the group $\zmods{\phi}$, i.e. $$ d = e\inv \md \phi. $$

Notice how computing the secret key $d$ would be impossible if we didn’t require $\gcd(e, \phi) = 1$, a necessary condition in order for $e$ to be invertible modulo $\phi$.

Encryption

Suppose Alice wants to encrypt a message $m$ and send the ciphertext $c = \enc(m)$ to Bob. Bob first generates a $(PK, SK)$ pair and provides Alice with the $PK = (n, e)$, which she uses to encrypt $m$ via $$ \enc(m) = m^e \mod n = c. $$

The key Alice uses does not need to be secret. Bob can provide this information over an insecure channel.

Decryption

Bob receives the ciphertext $c$ back from Alice, and uses his matching secret key $d$ to retrieve the plain text: $$ \dec(c) = c^d \mod n = m. $$

Notice how, although Bob can reveal $(n, e)$, he never reveals $\phi(n)$. Doing so would make it very easy to compute his secret key $d$ by inverting $e$.

Implementation

Java (BigInteger)

Java’s java.math.BigInteger class provides all the methods necessary for implementing unpadded RSA. To initialize the values for $p$ and $q$, one needs an instance of java.util.Random, then use the appropriate BigInteger constructor. Here are the necessary imports:

import java.math.BigInteger;
import java.util.Random;

Setup

The first step is initializing the RSA primes. If we want $n = pq$ to be $128$ bits long, the code would be:

int bits = 128;
int certainty = 20;
BigInteger ONE = BigInteger.ONE; //we use this a lot

r = new Random();

int adjustedBitLength = (int) Math.ceil(((double)bits)/2);
BigInteger p = new BigInteger(adjustedBitLength, certainty, r);
BigInteger q = new BigInteger(adjustedBitLength, certainty, r);

while (!q.compareTo(p) == 0) {
	q = new BigInteger(adjustedBigLength, certainty, r);
}

BigInteger n = p.multiply(q);
BigInteger phi = (p.subtract(ONE)).multiply(q.subtract(ONE));

Notice how we made $p$ and $q$ to be 64 bits each. This is to ensure that $n$ is 128-bit. In general, if we multiply an $a$-bit integer to a $b$-bit integer, the upper bound for the product is $$ (2^a - 1)(2^b - 1) = 2^{a+b} - 2^a - 2^b + 1 \leq 2^{a+b} - 1, $$ so it would require at most $a+b$ bits.

If we take a look at the documentation for the BigInteger class, we see that the certainty parameter influences the probability that the generated numbers are actually prime. In particular, the generated $p$ and $q$ are prime with probability $$ 1 - \frac{1}{2^\text{certainty}} $$

Because of the sheer size of the integers involved, it is computationally infeasible to actually try to factor $p$ and $q$ in order to ensure with 100% certainty that they are prime. Instead, some variation of the Miller–Rabin primality test is used to verify that these randomly chosen BigInteger are prime with some probability.

For example, a certainty value of 4 would yield a prime with 93.75% probability (very bad!). The primality test is not very expensive computationally, so we picked a default value of 20. However, for production-level security we would use something larger in the 50-100 range.

Key Generation

Since we want the public key $e$ to be in the group $\zmods{\phi}$, we generate a (positive) random BigInteger that occupies the same number of bits as $\phi$, until we find one from the group. The BigInteger class provides two methods for doing so, with slight differences:

• phi.bitCount(), which returns the number of bits in the two’s complement representation of $\phi$ that differ from its sign bit.
• phi.bitLength(), which returns the number of bits in the minimal two’s-complement representation of $\phi$, excluding a sign bit.

We want the second function. In the implementation, we actually have $e$ occupy one bit less than $\phi$, in the hopes to gain some speed and ensure we are inside the group. However, this is not the most secure approach.

BigInteger e = new BigInteger(phi.bitLength(), r);

while (e.compareTo(ONE) <= 0 || !phi.gcd(e).equals(ONE) || e.compareTo(phi) >= 0) {
	e = new BigInteger(phi.bitLength() - 1, r);
}

Finding the secret key is straightforward:

BigInteger d = e.modInverse(phi);

Encryption and Decryption

Once the system is set up, encrypting and decrypting are both very easy to implement. Suppose we wanted to encrypt the variable message, which is of type BigInteger. We’d do:

BigInteger ciphertext = message.modPow(e, n);

which can be recovered very easily by

BigInteger plaintext = ciphertext.modPow(d, n);

If we wanted to encrypt a message that is comprised of actual text (like an email), we’d have to first have a mapping between characters and numbers (e.g. their ASCII code), with padding so that each possible character encodings have the same size. Next, concatenate the encoded characters to obtain an encoded (but easily recoverable) message. Finally, break up the fully encoded message into equal sized blocks that are at most bits long (with padding if necessary), and encrypt each block using the code above. Implementing this is beyond the scope of this article, and is left to the reader.

Java with java-gmp

The GitHub repository includes a modified version of the code above which uses the java-gmp library for computing parts of the algorithm. In particular, prime generation, GCD, modular exponentiation, and modular inversion have all proven to be faster when using native GMP calls over Java’s BigInteger methods.

Here’s a comparison of executing times for RSA object initialization, as well as the encryption/decryption cycles, as calculated by the TestRSA.java class:

RSA creation (200 times):
   64 bits | Java: 43.66 ms | GMP: 17.05 ms
   128 bits | Java: 66.91 ms | GMP: 29.00 ms
   256 bits | Java: 369.9 ms | GMP: 70.31 ms
   512 bits | Java: 1.486 s | GMP: 313.0 ms
   1024 bits | Java: 6.608 s | GMP: 2.240 s
Done.
RSA encryption/decryption (1000 times):
   32 bits | Java: 4.751 ms | GMP: 5.070 ms
   64 bits | Java: 8.690 ms | GMP: 6.087 ms
   128 bits | Java: 25.43 ms | GMP: 9.753 ms
   256 bits | Java: 133.1 ms | GMP: 33.23 ms
   512 bits | Java: 689.3 ms | GMP: 137.6 ms
   1024 bits | Java: 3.854 s | GMP: 944.1 ms
   2048 bits | Java: 23.78 s | GMP: 7.682 s
Done.

Python (gmpy2)

RSA can be easily implemented in Python, but it is desirable to use a library that allows for multiple-precision integer arithmetic. One good option is gmpy2 (see documentation here). The following imports are necessary:

import gmpy2
from gmpy2 import mpz

Let’s set up the parameters for our encryption, and the necessary variables. For prime generation, gmpy2 also requires a random state object. Furthermore, we define a separate function to generate primes, making our code shorter:

bit_count = 64
rand_state = gmpy2.random_state(42)

def generate_prime(bits):
    temp = gmpy2.mpz_rrandomb(rand_state, bit_count)
    return gmpy2.next_prime(temp)

Below is the rest of the code, as well as encrypting and decrypting a test message:

# Setting up the encryption
#
p = generate_prime(bit_count)
q = generate_prime(bit_count)
assert(p != q)

n = gmpy2.mul(p, q)
phi = gmpy2.mul(p-1, q-1)

print("p:", p)
print("q:", q)
print("n:", n)
print("phi:", phi)


# Key Generation
#
# Choose 1 < e < phi such that gcd(e, phi) = 1
# e will be our Public Key
#
# Choose d the multiplicative inverse of e in Z/phi
# d will be our Secret Key
#
e = gmpy2.mpz_random(rand_state, phi)
while (e <= 1 or gmpy2.gcd(e, phi) != 1):
    e = gmpy2.mpz_random(rand_state, phi)
assert(e > 1)
assert(gmpy2.gcd(e, phi) == 1)

d = gmpy2.invert(e, phi)
assert(d != 1)
assert(gmpy2.t_mod(e*d, phi) == 1)

print("PK(e):", e)
print("SK(d):", d)


# Encryption and Decryption
#
m = mpz(123456789101112131415)
c = gmpy2.powmod(m, e, n)
m_rec = gmpy2.powmod(c, d, n)

print("Original message:", m)
print("Ciphertext:", c)
print("Recovered message:", m_rec)

Below is some sample output from the code:

p: 18446743798831775747
q: 13708957235651002373
n: 252885621875195130661895700184100847631
phi: 252885621875195130629739999149618069512
PK(e): 147179138790322486592026348258912295495
SK(d): 151999830484074365409582775016659113879
Original message: 123456789101112131415
Ciphertext: 95028871155225942543590774956453170196
Recovered message: 123456789101112131415

The Mathy Bit

Group Theoretic Results

Let’s go ahead and prove some of the mathematical theory behind the RSA. We assume the reader is familiar with basic concepts from group and ring theory. In particular, we provide Lagrange’s theorem without proof.

Lemma 1 (Lagrange’s theorem) If $G$ is a finite group, and $H$ is a subgroup of $G$, then $|H|$ divides $|G|$.

Lemma 2 If $G$ is a finite group and $a \in G$, then $a^{|G|} = e$, the identity element.

Proof. Let $H = \pra{a} = \prc{a^1, a^2, \dots, a^{r-1}, a^r = e}$ be the (cyclic) subgroup generated by $a$ of order $r$, and $n = |G|$. By Lagrange, we have $rk = n$ for some integer $k$, and so $$ a^{|G|} = a^{rk} = (a^r)^k = e^k = e. $$

Lemma 3 Let $G$ be a finite abelian group. Then for any $a \in G$ and any integer $k$, $$ a^{k} = a^{k \mod |G|} $$

Proof. Let $G$ be an abelian group of order $n$, and pick any $a \in G$. For any $k \in \Z$, we may write $k = nq+r$ for some $n, r \in \Z$. Notice that $k \equiv r \md n$, so $$ a^k = a^{nq+r} = a^{nq} a^r = e a^r = e^r = e^{k \mod |G|}. $$

Now that we have these prerequisites, let’s show that RSA is correct.

Correctness of RSA

The ciphertext is given by $c = m^e \mod n$. To see why the decryption algorithm recovers the message $m$, recall that $d \equiv e\inv \md{\phi(n)}$. In other words, $de \equiv 1 \md{\phi(n)}$ and we may write $de = 1 + k \phi(n)$ for some integer $k$. The decryption algorithm then gives $$ c^d \equiv (m^e)^d = m^{ed} = m^{1+k\phi(n)} = m \cdot (m^{\phi(n)})^k \md n, $$

and if $\gcd(m, n) = 1$, Euler’s theorem immediately gives the desired result, and RSA is correct for any message in the group $\zmods{n}$. But what if we want to work with the entire group $\zmod{n}$? After all, the original RSA paper doesn’t say anything about restricting the message space to elements coprime to $n$.

Suppose $m \in \zmod n$ and $\gcd(m, n) \neq 1$. Then one and only one of $p, q$ may divide $m$ (otherwise $m$ would be too large to belong to the group). Let’s assume WLOG that $\gcd(m, q) \neq 1$, but that $\gcd(m, p) = 1$.

By the Chinese Remainder Theorem, we have a ring isomorphism between $\zmod n$ and the direct product $\zmod p \times \zmod q$. In other words, every $m \in \zmod n$ corresponds to a unique solution to a system of congruences of the form $$ m \md n \longleftrightarrow \begin{cases} m \equiv a_p \md p \\ m \equiv a_q \md q \end{cases} $$

where $a_p \in \zmod p$ and $a_q \in \zmod q$. Since $q$ divides $m$, this system has a simpler form $$ m \md n \longleftrightarrow \begin{cases} m \equiv a_p \md p \\ m \equiv 0 \md q \end{cases} $$

Looking at $m^{ed}$, let’s show that it maps to the same system under our ring isomorphism. First, $m^{ed}$ reduces to 0 modulo $q$. What about modulo $p$? Notice that $$ m^{ed} \equiv a_p^{ed} \md p $$

where $a_p$ is nonzero, and thus relatively prime to $p$. Write $de = 1 + k(p-1)(q-1)$, which is congruent to $1$ modulo $\phi(p) = p-1$, which is the order of the group $\zmod p$. Invoking Lemma 3, we have $$ m^{ed} \equiv a_p^{ed} \equiv a^{ed \mod \phi(p)} \equiv a_p^1 = a_p \md p $$

Therefore $m^{ed}$ is the unique solution to the system $$ \begin{cases} m^{ed} \equiv a_p^{ed} \equiv a_p \md p \\ m^{ed} \equiv 0 \md q \end{cases} $$

which a priori had $m$ as a solution modulo $n$. Therefore $m^{ed} \equiv m \md n$, which concludes the correctness proof.

Fermat’s Little Theorem

For any prime $p$ and any integer $a$, we have $a^p \equiv a \md p$.

Proof. This is trivial for $a = 0$, so let’s assume $a$ is nonzero. Since $a^p \mod p = (a \mod p)^p$, we can work inside the multiplicative group $G = \prc{1, 2, \dots, p-1}$ of order $p-1$. Invoking Lemma 3, we have $$ a^p = a^{p-1} a \equiv a \md p $$ as desired.

Euler’s Theorem

Suppose $a$ and $n$ are coprime positive integers. Then $$ a^{\phi(n)} \equiv 1 \md n $$

Proof. As in the FLT proof, we work inside $\zmod n$, and since $\gcd(a, n) = 1$, we actually have $a \in \zmods n$, a multiplicative group of order $\phi(n)$. The result follows immediately from Lemma 3.

An alternate way to see this, without making use of Lemma 3, is to enumerate all the elements of the group $G = \zmods n$: $$ G = \prc{x_1, x_2, \dots, x_{\phi(n)}} $$

Taking $aG = \prc{ax_1, ax_2, \dots, ax_{\phi(n)}}$ has the effect of permuting the elements in $G$ (otherwise if $i \neq j$ and $ax_i = ax_j$, we’d have $x_i = x_j$, a contradiction), so $aG = G$ as sets. But then $$ \prod_{i=1}^{\phi(n)} x_i = \prod_{i=1}^{\phi(n)} ax_i = a^{\phi(n)}\prod_{i=1}^{\phi(n)} x_i $$

which implies $a^{\phi(n)}$ is the identity element in $G$.

Security of RSA

If the numbers $e, n$ are both very large, the ciphertext $c = m^e$ appears random and unrelated to $m$. However, RSA is deterministic (in the sense that encrypting the same $m$ always gives the same ciphertext), which allows an attacker to build a dictionary. There are other encryption schemes where this is not the case.

Another way an attacker can break RSA is to successfully factor $n$ as $p\cdot q$. Currently there is no known algorithm that can do this in polynomial time for large numbers (bigger than $10^{100}$). The best known general algorithm to date is the General Number Field Sieve, whose complexity is $$ \exp\pr{\pr{\sqrt[3]{\frac{64}{9}} + o(1)} b^{1/3} \pr{\ln b}^{2/3}} $$

for a number that is $b$ bits large. This algorithm is sub-exponential, but still super-polynomial.

In cryptography, there are formal definitions for correctness. We also have precise notions of semantic security (a way to measure the knowledge gain from a ciphertext when considering background knowledge) and ciphertext indistinguishability (which does not take into account background knowledge when measuring gain). It turns out the last two are equivalent.

While going into the details is beyond the scope of this article, it is worth mentioning that deterministic algorithms like RSA are not semantically secure. Even though $n$ cannot be factored in polynomial time, encrypting the message space using the public key is doable in polynomial time. Furthermore, unpadded RSA is not indistinguishable against eavesdropping attacks.

This issue does not exist for probabilistic encryption schemes like ElGamal, which we will discuss in a future article.